| Glossary |

First we start with an empty node. It contains just the dummy key. In this case the node is the root node and the keys are leaves.

The first few add cases are simple. Here, A
is added.

Now E
is added. The keys are kept in order. The dummy key always
comes last.

Another add, I
. The node is now full.
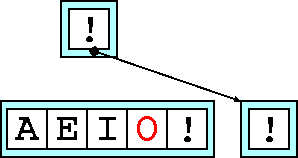
When we add O
, we find that the node overflows. We create two new nodes,
a parent and a sibling (on our right). We also find the median key, E
.
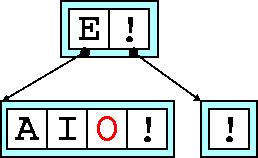
Next we promote the median key to the parent and attach ourselves as its child.
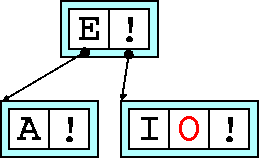
Finally we transfer all the keys greater than the median to the right-hand
sibling. The operation is complete. We now have a new root node, containing
E
. The leaves (keys with no children) are A
, I
and
O
.
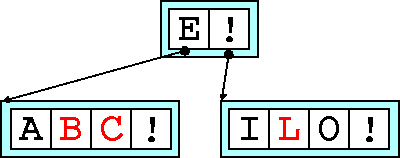
After adding B
, C
and L
both the children nodes are now
full.
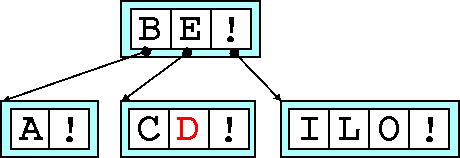
Adding D
we overfill the node. This time we already have a parent, so
when we promote the median, B
, to the parent. We will always need a
new right-hand sibling.
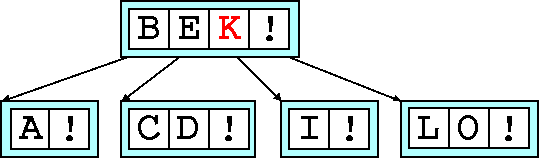
Here we add K
and we find that the newly inserted key is the median
itself. This is no different.
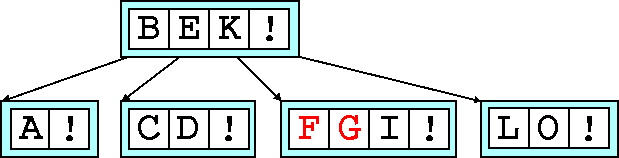
Fill another node with F
and G
for the final example.
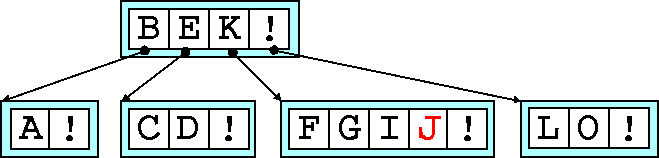
We add J
but the node is too full, so we promote G
and split the
node.
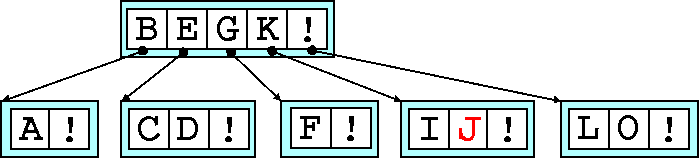
Unfortunately, the node we've just promoted a key too is now too full. So
we'll have to split that node as well. The median is E
.
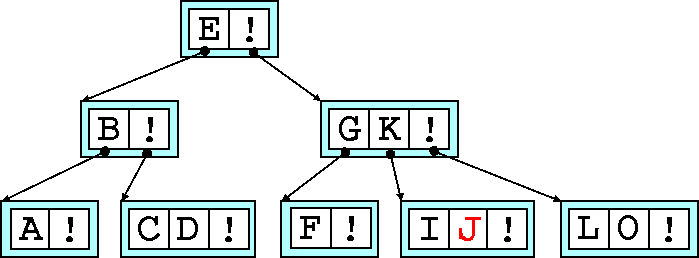
Ignoring the children of this node, this promotion is exactly like the promotion in Figures 5,6,7. Now the tree is 3 nodes deep.
Now have a look at the delete cases.